模型集成¶

以下是 Darts 中集成模型的简要演示。从快速入门笔记本中提供的示例开始，将详细介绍一些高级特性和细节。

本笔记本涵盖以下主题： * 基础知识与参考 * 朴素集成 * 确定性 * 协变量与多变量序列 * 概率性 * 学习型集成 * 确定性 * 概率性 * Bootstrap * 预训练集成

[1]:

# fix python path if working locally
from utils import fix_pythonpath_if_working_locally

fix_pythonpath_if_working_locally()

[2]:

%load_ext autoreload
%autoreload 2
%matplotlib inline
import warnings

import matplotlib.pyplot as plt

from darts.dataprocessing.transformers import Scaler
from darts.datasets import AirPassengersDataset
from darts.metrics import mape
from darts.models import (
    ExponentialSmoothing,
    KalmanForecaster,
    LinearRegressionModel,
    NaiveDrift,
    NaiveEnsembleModel,
    NaiveSeasonal,
    RandomForest,
    RegressionEnsembleModel,
    TCNModel,
)
from darts.utils.timeseries_generation import (
    datetime_attribute_timeseries as dt_attr,
)

warnings.filterwarnings("ignore")

import logging

logging.disable(logging.CRITICAL)

基础知识与参考¶

集成结合了几个“弱”模型的预测，以获得更鲁棒和更准确的模型。

所有 Darts 集成模型都依赖于 堆叠技术 (参考)。它们提供与其他预测模型相同的功能。根据集成的模型，它们可以

利用协变量
在多个序列上训练
预测多变量目标
生成概率预测
等等…

[3]:

# using the AirPassenger dataset, directly available in darts
ts_air = AirPassengersDataset().load()
ts_air.plot()

[3]:

<Axes: xlabel='Month'>

../_images/examples_19-EnsembleModel-examples_4_1.png

朴素集成¶

朴素集成简单地取集成预测模型生成的预测结果的平均值。Darts 的 NaiveEnsembleModel 接受局部和全局预测模型（以及两者的组合，但有一些额外的限制）。

[4]:

naive_ensemble = NaiveEnsembleModel(
    forecasting_models=[NaiveSeasonal(K=12), NaiveDrift()]
)

backtest = naive_ensemble.historical_forecasts(ts_air, start=0.6, forecast_horizon=3)

ts_air.plot(label="series")
backtest.plot(label="prediction")
print("NaiveEnsemble (naive) MAPE:", round(mape(backtest, ts_air), 5))

NaiveEnsemble (naive) MAPE: 11.87818

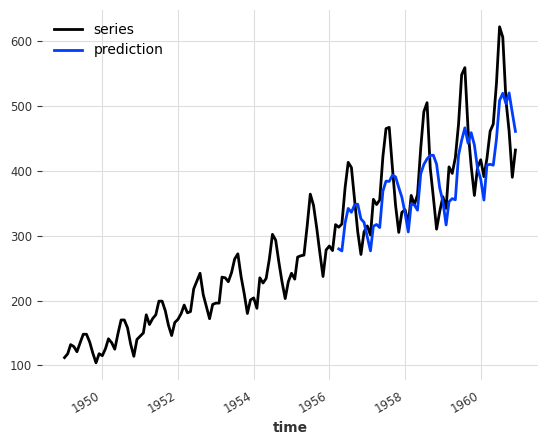
../_images/examples_19-EnsembleModel-examples_6_1.png

注意：在查看每个模型的 MAPE 后，您会注意到 NaiveSeasonal 单独使用时实际上比与 NaiveDrift 集成时表现更好。在定义集成模型之前，检查单个模型的性能通常是一个好习惯。

在创建新的 NaiveEnsemble 之前，我们将筛选模型，以确定哪些模型可以很好地协同工作。候选模型包括： - LinearRegressionModel：经典简单模型 - ExponentialSmoothing：移动窗口模型 - KalmanForecaster：基于滤波器的模型 - RandomForest：决策树模型

[5]:

candidates_models = {
    "LinearRegression": (LinearRegressionModel, {"lags": 12}),
    "ExponentialSmoothing": (ExponentialSmoothing, {}),
    "KalmanForecaster": (KalmanForecaster, {"dim_x": 12}),
    "RandomForest": (RandomForest, {"lags": 12, "random_state": 0}),
}

backtest_models = []

for model_name, (model_cls, model_kwargs) in candidates_models.items():
    model = model_cls(**model_kwargs)
    backtest_models.append(
        model.historical_forecasts(ts_air, start=0.6, forecast_horizon=3)
    )
    print(f"{model_name} MAPE: {round(mape(backtest_models[-1], ts_air), 5)}")

LinearRegression MAPE: 4.64008
ExponentialSmoothing MAPE: 4.44874
KalmanForecaster MAPE: 4.5539
RandomForest MAPE: 8.02264

[6]:

fix, axes = plt.subplots(2, 2, figsize=(9, 6))
for ax, backtest, model_name in zip(
    axes.flatten(),
    backtest_models,
    list(candidates_models.keys()),
):
    ts_air[-len(backtest) :].plot(ax=ax, label="ground truth")
    backtest.plot(ax=ax, label=model_name)

    ax.set_title(model_name)
    ax.set_ylim([250, 650])
plt.tight_layout()

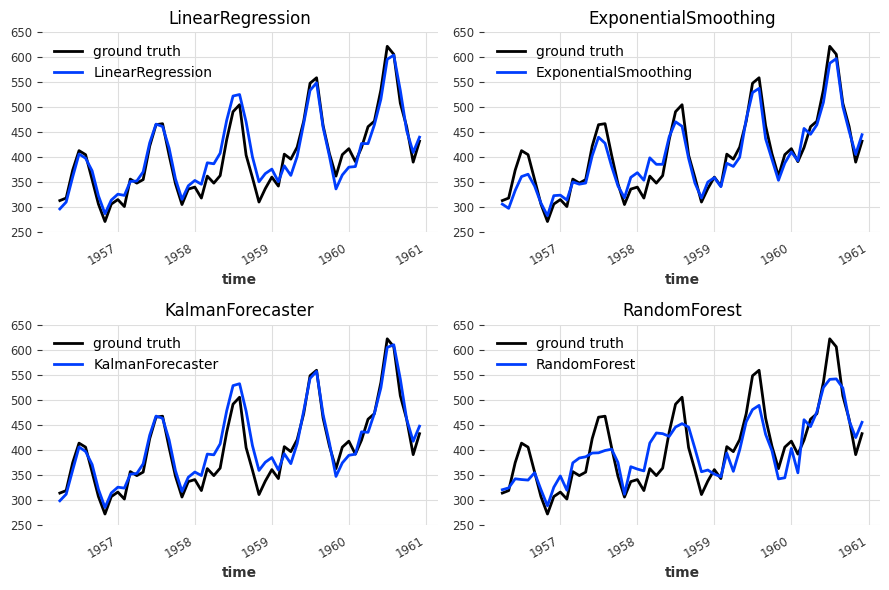
../_images/examples_19-EnsembleModel-examples_9_0.png

使用 LinearRegressionModel 和 KalmanForecaster 获得的预测结果看起来非常相似，而 ExponentialSmoothing 倾向于低估真实值，RandomForest 未能捕捉到峰值。为了从集成中获益，我们将倾向于多样性，并继续使用 LinearRegressionModel 和 ExponentialSmoothing。

[7]:

ensemble = NaiveEnsembleModel(
    forecasting_models=[LinearRegressionModel(lags=12), ExponentialSmoothing()]
)

backtest = ensemble.historical_forecasts(ts_air, start=0.6, forecast_horizon=3)

ts_air[-len(backtest) :].plot(label="series")
backtest.plot(label="prediction")
plt.ylim([250, 650])
print("NaiveEnsemble (v2) MAPE:", round(mape(backtest, ts_air), 5))

NaiveEnsemble (v2) MAPE: 4.04297

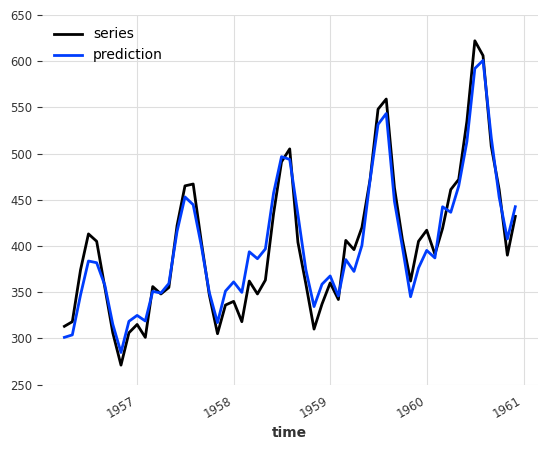
../_images/examples_19-EnsembleModel-examples_11_1.png

与单个模型 MAPE 分数相比，LinearRegressionModel 的 MAPE 为 4.64008，ExponentialSmoothing 的 MAPE 为 4.44874，集成模型的准确性提高到 4.04297！

使用协变量与预测多变量序列¶

根据使用的预测模型，EnsembleModel 当然也可以利用协变量或预测多变量序列！协变量只会传递给支持它们的预测模型。

在下面的示例中，ExponentialSmoothing 模型不支持任何协变量，而 LinearRegressionModel 模型支持 future_covariates。

[8]:

ensemble = NaiveEnsembleModel([
    LinearRegressionModel(lags=12, lags_future_covariates=[0]),
    ExponentialSmoothing(),
])

# encoding the months as integer, normalised
future_cov = dt_attr(ts_air.time_index, "month", add_length=12) / 12
backtest = ensemble.historical_forecasts(
    ts_air, future_covariates=future_cov, start=0.6, forecast_horizon=3
)

ts_air[-len(backtest) :].plot(label="series")
backtest.plot(label="prediction")
plt.ylim([250, 650])
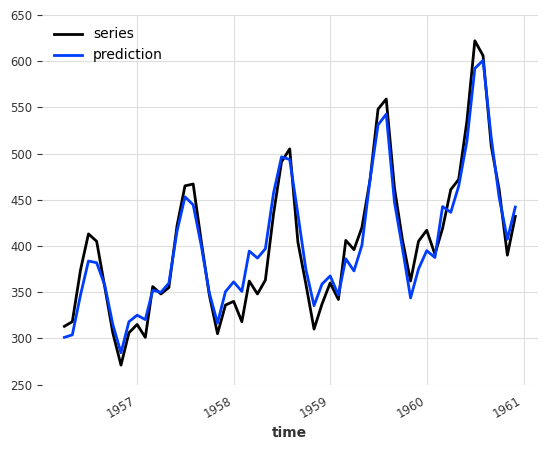
print("NaiveEnsemble (w/ future covariates) MAPE:", round(mape(backtest, ts_air), 5))

NaiveEnsemble (w/ future covariates) MAPE: 4.07502

../_images/examples_19-EnsembleModel-examples_13_1.png

概率朴素集成¶

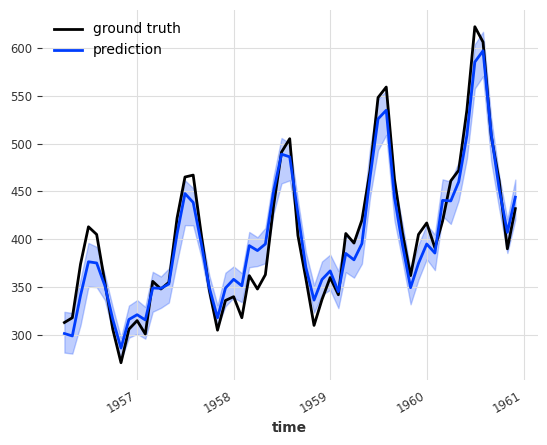
结合支持概率预测的模型会得到一个概率 NaiveEnsembleModel！我们可以轻松调整上面使用的模型，使它们具有概率性，并在预测中获得置信区间

[9]:

ensemble_probabilistic = NaiveEnsembleModel(
    forecasting_models=[
        LinearRegressionModel(
            lags=12,
            likelihood="quantile",
            quantiles=[0.05, 0.5, 0.95],
        ),
        ExponentialSmoothing(),
    ]
)

# must pass num_samples > 1 to obtain a probabilistic forecasts
backtest = ensemble_probabilistic.historical_forecasts(
    ts_air, start=0.6, forecast_horizon=3, num_samples=100
)

ts_air[-len(backtest) :].plot(label="ground truth")
backtest.plot(label="prediction")

[9]:

<Axes: xlabel='time'>

../_images/examples_19-EnsembleModel-examples_15_1.png

学习型集成¶

集成也可以被视为一个监督回归问题：给定一组预测（特征），找到一个模型来组合它们，以最小化目标上的误差。这就是 RegressionEnsembleModel 所做的事情。主要有三个参数：

forecasting_models 是一个预测模型的列表，我们希望集成它们的预测结果。
regression_train_n_points 是用于拟合“集成回归”模型（即组合预测结果的内部模型）的时间步数。
regression_model 是可选的，可以是 sklearn 兼容的回归模型，或是用于集成回归的 Darts RegressionModel。如果未指定，则使用 Darts 的 LinearRegressionModel。使用 sklearn 模型很容易，但使用 Darts 的回归模型可以潜在地将单个预测结果的任意滞后作为回归模型的输入。

一旦这些元素到位，RegressionEnsembleModel 就可以像常规预测模型一样使用

[10]:

ensemble_model = RegressionEnsembleModel(
    forecasting_models=[NaiveSeasonal(K=12), NaiveDrift()],
    regression_train_n_points=12,
)

backtest = ensemble_model.historical_forecasts(ts_air, start=0.6, forecast_horizon=3)

ts_air.plot()
backtest.plot()

print("RegressionEnsemble (naive) MAPE:", round(mape(backtest, ts_air), 5))

RegressionEnsemble (naive) MAPE: 4.85142

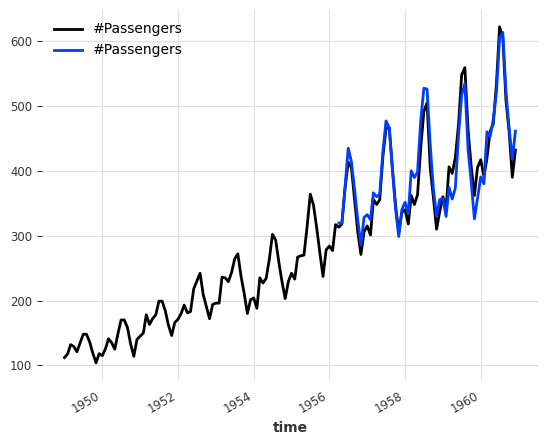
../_images/examples_19-EnsembleModel-examples_17_1.png

与朴素集成部分开头获得的 MAPE 11.87818 相比，在两个朴素模型之上添加一个 LinearRegressionModel 确实提高了预测质量。

现在，让我们看看当 RegressionEnsemble 的预测模型不是朴素模型时，是否能观察到类似的提升

[11]:

ensemble = RegressionEnsembleModel(
    forecasting_models=[LinearRegressionModel(lags=12), ExponentialSmoothing()],
    regression_train_n_points=12,
)

backtest = ensemble.historical_forecasts(ts_air, start=0.6, forecast_horizon=3)

ts_air.plot(label="series")
backtest.plot(label="prediction")

print("RegressionEnsemble (v2) MAPE:", round(mape(backtest, ts_air), 5))

RegressionEnsemble (v2) MAPE: 4.63334

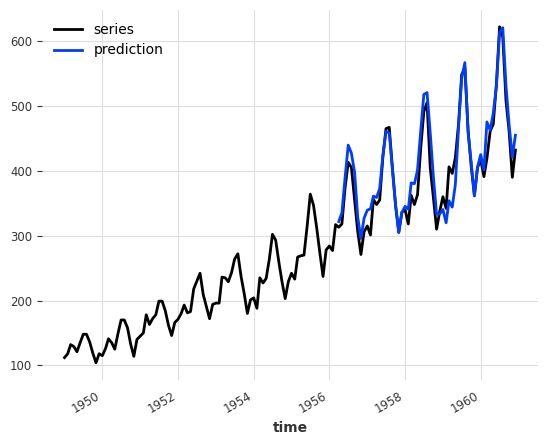
../_images/examples_19-EnsembleModel-examples_19_1.png

有趣的是，即使与依赖朴素模型的 RegressionEnsemble 相比 MAPE 有所改善（MAPE：4.85142），它也并未优于使用类似预测模型的 NaiveEnsemble（MAPE：4.04297）。

这种性能差距部分是由于用于训练集成 LinearRegression 的点被留出；两个预测模型（LinearRegression 和 ExponentialSmoothing）无法访问序列的最新值，而这些最新值包含明显的上升趋势。

出于好奇，我们可以使用 sklearn 库中的 Ridge 回归模型来集成预测结果

[12]:

from sklearn.linear_model import Ridge

ensemble = RegressionEnsembleModel(
    forecasting_models=[LinearRegressionModel(lags=12), ExponentialSmoothing()],
    regression_train_n_points=12,
    regression_model=Ridge(),
)

backtest = ensemble.historical_forecasts(ts_air, start=0.6, forecast_horizon=3)

print("RegressionEnsemble (Ridge) MAPE:", round(mape(backtest, ts_air), 5))

RegressionEnsemble (Ridge) MAPE: 6.46803

在这种特定情况下，使用带有正则化项的回归模型恶化了预测结果，但在其他情况下它可能会有所改进。

使用历史预测进行训练¶

当预测的数量大于其 output_chunk_length 时，GlobalForecastingModels 依赖自回归（使用自身的输出作为输入）来预测远期值。然而，随着预测时间戳距离观测结束越远，预测质量会显著下降。在 RegressionEnsemble 的回归模型训练期间，预测模型会为已知真实值的 timestamps 生成预测，这使得可以使用 historical_forecasts 代替 predict()。

可以通过设置 train_using_historical_forecasts=True 来启用此功能。

在内部，集成模型将为每个模型触发历史预测，设置 forecast_horizon=model.output_chunk_length、stride=model.output_chunk_length、last_points_only=False 和 overlap_end=False，以预测目标序列的最后 regression_train_n_points 个点。

[13]:

# replacing the ExponentialSmoothing (local) with RandomForest (global)
ensemble = RegressionEnsembleModel(
    forecasting_models=[
        LinearRegressionModel(lags=12),
        RandomForest(lags=12, random_state=0),
    ],
    regression_train_n_points=12,
    train_using_historical_forecasts=False,
)
backtest = ensemble.historical_forecasts(ts_air, start=0.6, forecast_horizon=3)

ensemble_hist_fct = RegressionEnsembleModel(
    forecasting_models=[
        LinearRegressionModel(lags=12),
        RandomForest(lags=12, random_state=0),
    ],
    regression_train_n_points=12,
    train_using_historical_forecasts=True,
)
backtest_hist_fct = ensemble_hist_fct.historical_forecasts(
    ts_air, start=0.6, forecast_horizon=3
)

print("RegressionEnsemble (no hist_fct) MAPE:", round(mape(backtest, ts_air), 5))
print("RegressionEnsemble (hist_fct) MAPE:", round(mape(backtest_hist_fct, ts_air), 5))

RegressionEnsemble (no hist_fct) MAPE: 5.7016
RegressionEnsemble (hist_fct) MAPE: 5.12017

正如预期，使用历史预测和预测模型来训练回归模型会产生更好的预测结果。

概率回归集成¶

为了具有概率性，RegressionEnsembleModel 必须包含一个概率集成回归模型（参见 README 中的表格）

[14]:

ensemble = RegressionEnsembleModel(
    forecasting_models=[LinearRegressionModel(lags=12), ExponentialSmoothing()],
    regression_train_n_points=12,
    regression_model=LinearRegressionModel(
        lags_future_covariates=[0], likelihood="quantile", quantiles=[0.05, 0.5, 0.95]
    ),
)

backtest = ensemble.historical_forecasts(
    ts_air, start=0.6, forecast_horizon=3, num_samples=100
)

ts_air[-len(backtest) :].plot(label="ground truth")
backtest.plot(label="prediction")

print("RegressionEnsemble (probabilistic) MAPE:", round(mape(backtest, ts_air), 5))

RegressionEnsemble (probabilistic) MAPE: 5.15071

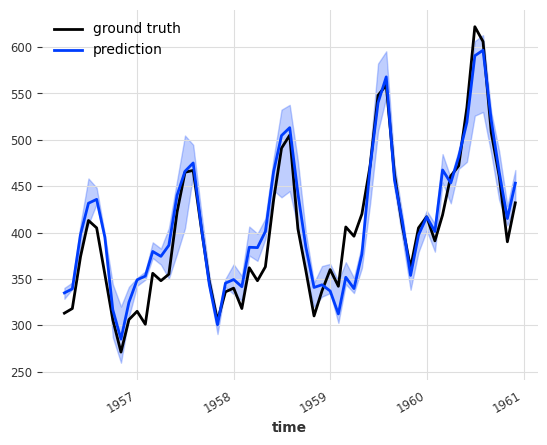
../_images/examples_19-EnsembleModel-examples_25_1.png

Bootstrap 回归集成¶

当 RegressionEnsembleModel 的预测模型具有概率性时，其预测结果的样本维度会被降维，并用作集成回归的协变量。由于集成回归模型是确定性的，生成的预测结果也是确定性的。

[15]:

ensemble = RegressionEnsembleModel(
    forecasting_models=[
        LinearRegressionModel(
            lags=12, likelihood="quantile", quantiles=[0.05, 0.5, 0.95]
        ),
        ExponentialSmoothing(),
    ],
    regression_train_n_points=12,
    regression_train_num_samples=100,
    regression_train_samples_reduction="median",
)

backtest = ensemble.historical_forecasts(ts_air, start=0.6, forecast_horizon=3)

ts_air[-len(backtest) :].plot(label="ground truth")
backtest.plot(label="prediction")

print("RegressionEnsemble (bootstrap) MAPE:", round(mape(backtest, ts_air), 5))

RegressionEnsemble (bootstrap) MAPE: 5.10138

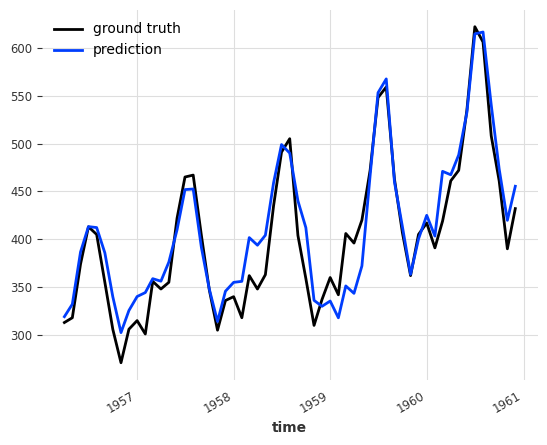
../_images/examples_19-EnsembleModel-examples_27_1.png

预训练集成¶

由于 NaiveEnsembleModel 和 RegressionEnsembleModel 都接受 GlobalForecastingModel 作为预测模型，因此它们可以用于集成预训练的深度学习和回归模型。请注意，此功能仅在所有集成预测模型都是 GlobalForecastingModel 类的实例，并且在创建集成时已经训练好时才受支持。

免责声明：请注意不要使用验证期间使用的数据来预训练模型，因为这会引入相当大的偏差。

注意：TCNModel 的参数很大程度上借鉴了 TCNModel 示例笔记本。

[16]:

# holding out values for validation
train, val = ts_air.split_after(0.8)

# scaling the target
scaler = Scaler()
train = scaler.fit_transform(train)
val = scaler.transform(val)

# use the month as a covariate
month_series = dt_attr(ts_air.time_index, attribute="month", one_hot=True)
scaler_month = Scaler()
month_series = scaler_month.fit_transform(month_series)

# training a regular linear regression, without any covariates
linreg_model = LinearRegressionModel(lags=24)
linreg_model.fit(train)

# instanciating a TCN model with parameters optimized for the AirPassenger dataset
tcn_model = TCNModel(
    input_chunk_length=24,
    output_chunk_length=12,
    n_epochs=500,
    dilation_base=2,
    weight_norm=True,
    kernel_size=5,
    num_filters=3,
    random_state=0,
)
tcn_model.fit(train, past_covariates=month_series)

[16]:

TCNModel(kernel_size=5, num_filters=3, num_layers=None, dilation_base=2, weight_norm=True, dropout=0.2, input_chunk_length=24, output_chunk_length=12, n_epochs=500, random_state=0)

作为健全性检查，我们将单独查看每个模型的预测结果

[17]:

# individual model forecasts
pred_linreg = linreg_model.predict(24)
pred_tcn = tcn_model.predict(24, verbose=False)

# scaling them back
pred_linreg_rescaled = scaler.inverse_transform(pred_linreg)
pred_tcn_rescaled = scaler.inverse_transform(pred_tcn)

# plotting
ts_air[-24:].plot(label="ground truth")
pred_linreg_rescaled.plot(label="LinearRegressionModel")
pred_tcn_rescaled.plot(label="TCNModel")
plt.show()

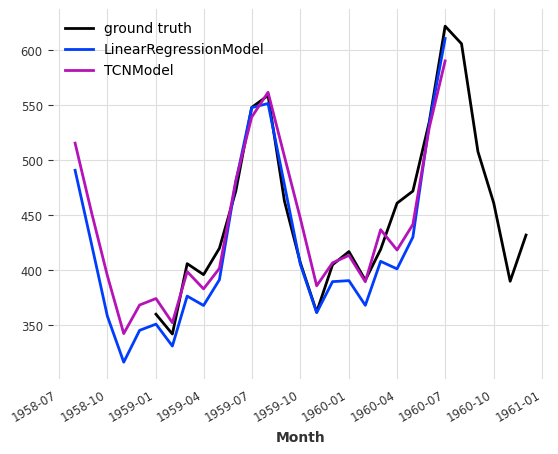
../_images/examples_19-EnsembleModel-examples_31_0.png

现在我们对这些模型的单个性能有了很好的了解，可以对它们进行集成了。必须确保设置 train_forecasting_models=False，否则集成模型在调用 predict() 之前需要先进行拟合。

建议：使用 save() 方法导出您的模型并保留您的权重副本。

[18]:

naive_ensemble = NaiveEnsembleModel(
    forecasting_models=[tcn_model, linreg_model], train_forecasting_models=False
)
# NaiveEnsemble initialized with pre-trained models can call predict() directly,
# the `series` argument must however be provided
pred_naive = naive_ensemble.predict(len(val), train)

pretrain_ensemble = RegressionEnsembleModel(
    forecasting_models=[tcn_model, linreg_model],
    regression_train_n_points=24,
    train_forecasting_models=False,
    train_using_historical_forecasts=False,
)
# RegressionEnsemble must train the ensemble model, even if the forecasting models are already trained
pretrain_ensemble.fit(train)
pred_ens = pretrain_ensemble.predict(len(val))

# scaling back the predictions
pred_naive_rescaled = scaler.inverse_transform(pred_naive)
pred_ens_rescaled = scaler.inverse_transform(pred_ens)

# plotting
plt.figure(figsize=(8, 5))
scaler.inverse_transform(val).plot(label="ground truth")
pred_naive_rescaled.plot(label="pre-trained NaiveEnsemble")
pred_ens_rescaled.plot(label="pre-trained RegressionEnsemble")
plt.ylim([250, 650])

# MAPE
print("LinearRegression MAPE:", round(mape(pred_linreg_rescaled, ts_air), 5))
print("TCNModel MAPE:", round(mape(pred_tcn_rescaled, ts_air), 5))
print("NaiveEnsemble (pre-trained) MAPE:", round(mape(pred_naive_rescaled, ts_air), 5))
print(
    "RegressionEnsemble (pre-trained) MAPE:", round(mape(pred_ens_rescaled, ts_air), 5)
)

LinearRegression MAPE: 3.91311
TCNModel MAPE: 4.70491
NaiveEnsemble (pre-trained) MAPE: 3.82837
RegressionEnsemble (pre-trained) MAPE: 3.61749

../_images/examples_19-EnsembleModel-examples_33_1.png

结论¶

集成预训练的 LinearRegression 和 TCNModel 模型使我们能够超越单个模型，并且在预测结果之上训练线性回归模型进一步提高了 MAPE 分数。

虽然在这个小型数据集上的收益有限，但集成是一种强大的技术，可以产生令人印象深刻的结果，并且在 Makridakis 竞赛第四届的获胜者中得到了显著应用（网站，github 仓库）。

时间序列混合器 (TSMixer)

使用 Darts 滤波器进行滤波和预测