电力负荷预测的超参数优化¶
在本 notebook 中,我们将演示如何使用深度学习预测模型进行超参数优化,以便准确预测电力负荷并提供置信区间。
我们将使用此数据集(在 darts.datasets 中即可获取),其中包含一家葡萄牙能源公司的 370 位客户的电力消耗测量数据,频率为 15 分钟。我们将尝试预测未来 2 周。在此频率下,这意味着我们将尝试预测未来 2,688 个时间步。这是一个相当苛刻的要求,我们将尝试找到一个好模型来完成此任务。
我们将使用开源 Optuna 库进行超参数优化,并使用 Darts 的 TCN 模型(参阅此处获取此模型的入门文章)。此模型采用扩张卷积,在捕获如此高频率(15 分钟)长时间(数周)序列的同时保持模型整体尺寸较小方面效果极佳。
建议使用 GPU 运行此 notebook,尽管所有概念无论模型运行在 CPU 还是 GPU 上都适用。
首先,我们安装并导入所需的库
[ ]:
# necessary packages:
!pip install -U darts
!pip install -U optuna
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import optuna
import torch
from optuna.integration import PyTorchLightningPruningCallback
from optuna.visualization import (
plot_contour,
plot_optimization_history,
plot_param_importances,
)
from pytorch_lightning.callbacks import EarlyStopping
from sklearn.preprocessing import MaxAbsScaler
from tqdm.notebook import tqdm
from darts.dataprocessing.transformers import Scaler
from darts.datasets import ElectricityDataset
from darts.metrics import smape
from darts.models import LinearRegressionModel, TCNModel
from darts.utils.likelihood_models.torch import GaussianLikelihood
数据准备¶
以下单元格可能需要几分钟才能执行完成。它将从互联网下载约 250 MB 的数据。我们指定 multivariate=False,因此我们获得 370 个单变量 TimeSeries 的列表。我们也可以指定 multivariate=True 以获得一个包含 370 个分量的多变量 TimeSeries。
[2]:
all_series = ElectricityDataset(multivariate=False).load()
我们保留每个序列的最后 80 天数据,并将它们全部转换为 float32 类型
[3]:
NR_DAYS = 80
DAY_DURATION = 24 * 4 # 15 minutes frequency
all_series_fp32 = [
s[-(NR_DAYS * DAY_DURATION) :].astype(np.float32) for s in tqdm(all_series)
]
我们有 370 个单变量 TimeSeries,每个的时间频率为 15 分钟。接下来,我们将在所有这些序列上训练一个单一的全局模型。
首先,我们创建训练集。我们将最后 14 天的数据作为测试集,并将之前的 14 天作为验证集(用于超参数优化)。
请注意,下面的 val 和 test 集仅包含序列中 14 天的“预测评估”部分。在本 notebook 中,我们将评估一些 14 天预测在 val(或 test)上的准确性。然而,为了生成这些 14 天的预测,我们的模型将需要消耗一定长度的回溯窗口 in_len 的时间戳。因此,下面我们还将创建包含这些额外 in_len 点的验证集(由于 in_len 本身是一个超参数,我们动态创建这些更长的验证集);这主要用于早停。
[4]:
# Split in train/val/test
val_len = 14 * DAY_DURATION # 14 days
train = [s[: -(2 * val_len)] for s in all_series_fp32]
val = [s[-(2 * val_len) : -val_len] for s in all_series_fp32]
test = [s[-val_len:] for s in all_series_fp32]
# Scale so that the largest value is 1.
# This way of scaling perserves the sMAPE
scaler = Scaler(scaler=MaxAbsScaler())
train = scaler.fit_transform(train)
val = scaler.transform(val)
test = scaler.transform(test)
让我们绘制一些序列
[5]:
for i in [10, 50, 100, 150, 250, 350]:
plt.figure(figsize=(15, 5))
train[i].plot(label=f"{i}")
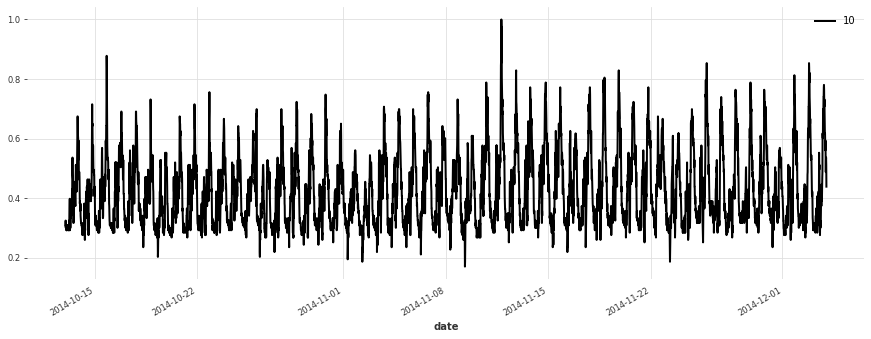
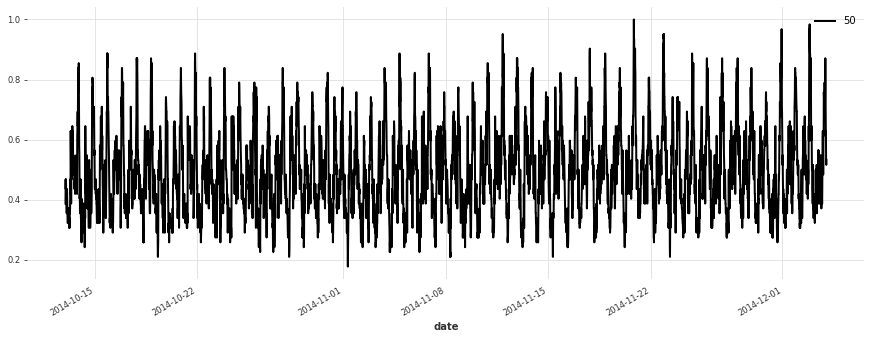
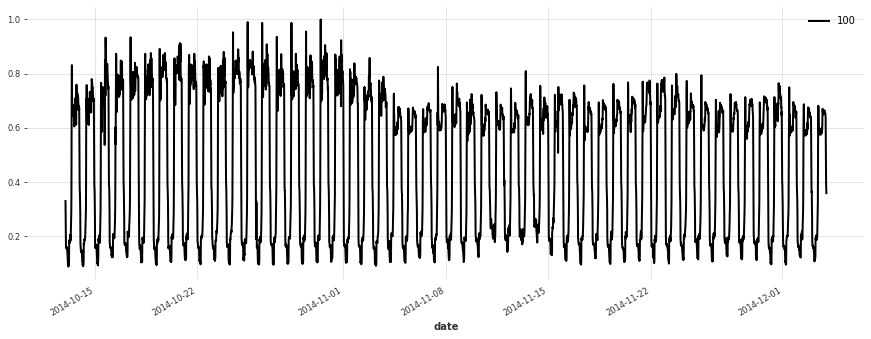

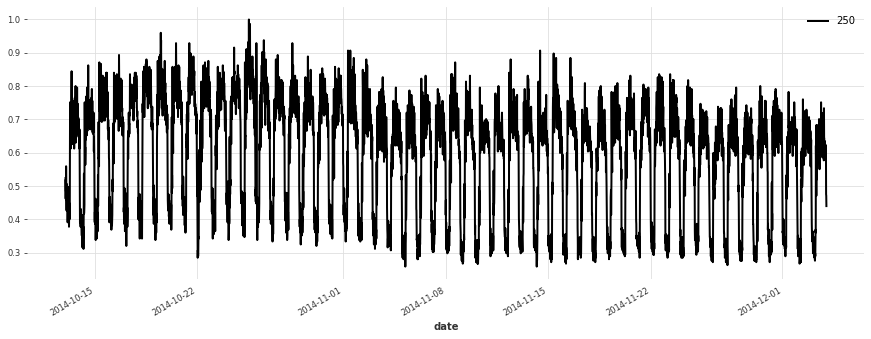

构建简单的线性模型¶
我们首先不进行任何超参数优化,尝试一个简单的线性回归模型。它将作为基线。在此模型中,我们使用 1 周的回溯窗口。
注意:要比线性回归表现好得多通常并非易事!我们建议在转向更复杂的模型之前,始终先考虑至少一个这样合理的简单基线。
LinearRegressionModel 封装了 sklearn.linear_model.LinearRegression,这可能需要大量的处理和内存。运行此单元格需要几分钟,除非您的系统至少有 20GB RAM,否则我们建议跳过它。
[6]:
lr_model = LinearRegressionModel(lags=7 * DAY_DURATION)
lr_model.fit(train);
让我们看看这个模型的表现如何
[7]:
def eval_model(preds, name, train_set=train, val_set=val):
smapes = smape(preds, val_set)
print(f"{name} sMAPE: {np.mean(smapes):.2f} +- {np.std(smapes):.2f}")
for i in [10, 50, 100, 150, 250, 350]:
plt.figure(figsize=(15, 5))
train_set[i][-7 * DAY_DURATION :].plot()
val_set[i].plot(label="actual")
preds[i].plot(label="forecast")
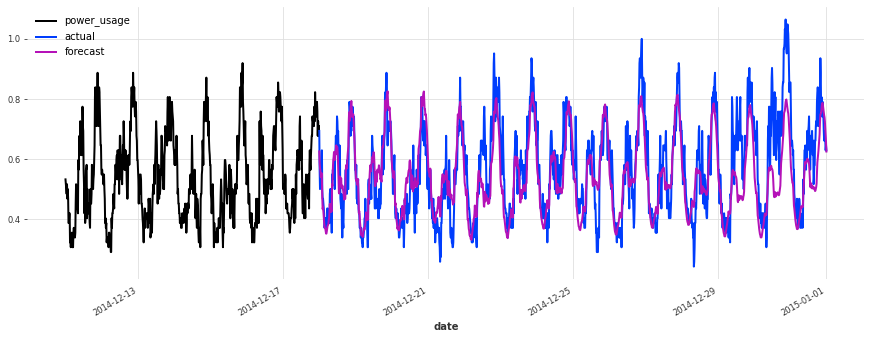
lr_preds = lr_model.predict(series=train, n=val_len)
eval_model(lr_preds, "linear regression")
linear regression sMAPE: 16.01 +- 20.59
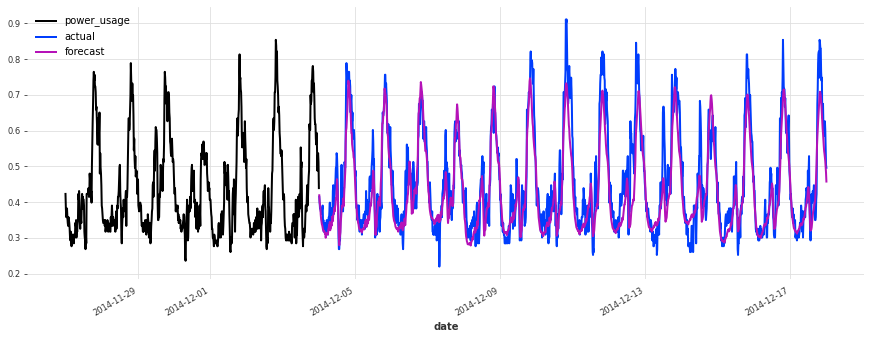
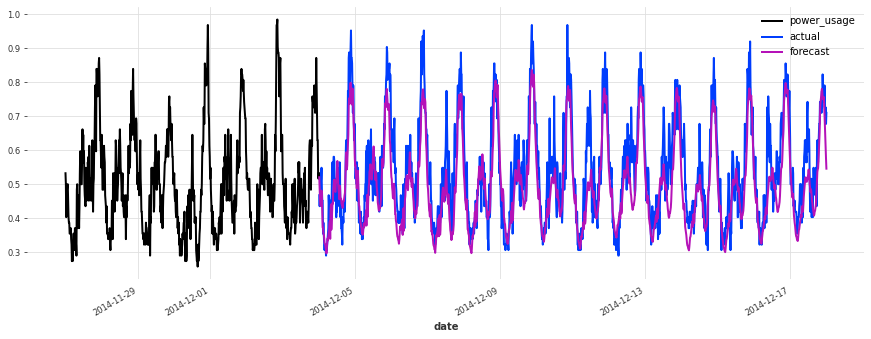
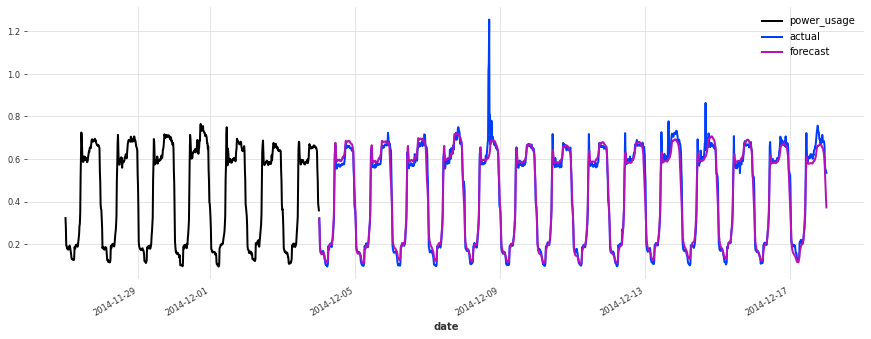
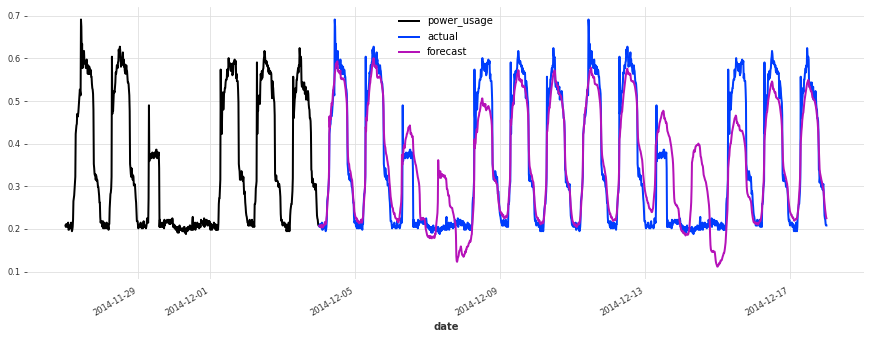
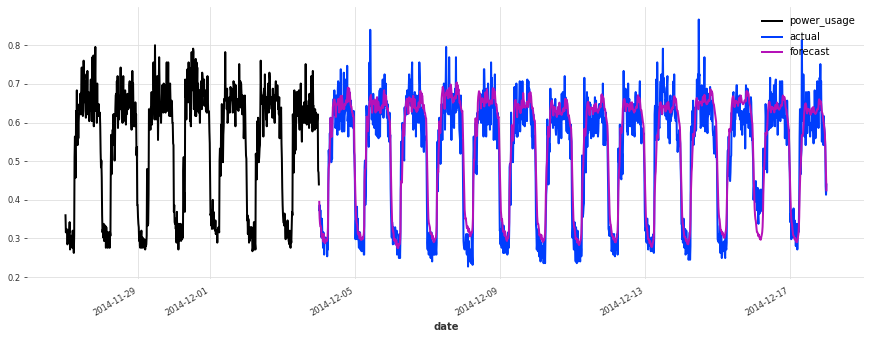
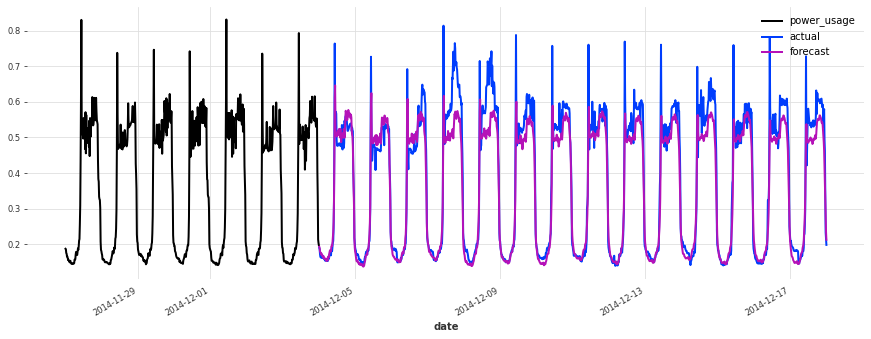
这个模型开箱即用,表现相当不错!现在让我们看看是否可以使用深度学习做得更好。
构建简单的 TCN 模型¶
现在我们构建一个使用一些简单超参数选择的 TCN 模型,但不进行任何超参数优化。
[8]:
""" We write a function to build and fit a TCN Model, which we will re-use later.
"""
def build_fit_tcn_model(
in_len,
out_len,
kernel_size,
num_filters,
weight_norm,
dilation_base,
dropout,
lr,
include_dayofweek,
likelihood=None,
callbacks=None,
):
# reproducibility
torch.manual_seed(42)
# some fixed parameters that will be the same for all models
BATCH_SIZE = 1024
MAX_N_EPOCHS = 30
NR_EPOCHS_VAL_PERIOD = 1
MAX_SAMPLES_PER_TS = 1000
# throughout training we'll monitor the validation loss for early stopping
early_stopper = EarlyStopping("val_loss", min_delta=0.001, patience=3, verbose=True)
if callbacks is None:
callbacks = [early_stopper]
else:
callbacks = [early_stopper] + callbacks
# detect if a GPU is available
if torch.cuda.is_available():
pl_trainer_kwargs = {
"accelerator": "gpu",
"gpus": -1,
"auto_select_gpus": True,
"callbacks": callbacks,
}
num_workers = 4
else:
pl_trainer_kwargs = {"callbacks": callbacks}
num_workers = 0
# optionally also add the day of the week (cyclically encoded) as a past covariate
encoders = {"cyclic": {"past": ["dayofweek"]}} if include_dayofweek else None
# build the TCN model
model = TCNModel(
input_chunk_length=in_len,
output_chunk_length=out_len,
batch_size=BATCH_SIZE,
n_epochs=MAX_N_EPOCHS,
nr_epochs_val_period=NR_EPOCHS_VAL_PERIOD,
kernel_size=kernel_size,
num_filters=num_filters,
weight_norm=weight_norm,
dilation_base=dilation_base,
dropout=dropout,
optimizer_kwargs={"lr": lr},
add_encoders=encoders,
likelihood=likelihood,
pl_trainer_kwargs=pl_trainer_kwargs,
model_name="tcn_model",
force_reset=True,
save_checkpoints=True,
)
# when validating during training, we can use a slightly longer validation
# set which also contains the first input_chunk_length time steps
model_val_set = scaler.transform([
s[-((2 * val_len) + in_len) : -val_len] for s in all_series_fp32
])
# train the model
model.fit(
series=train,
val_series=model_val_set,
max_samples_per_ts=MAX_SAMPLES_PER_TS,
dataloader_kwargs={"num_workers": num_workers},
)
# reload best model over course of training
model = TCNModel.load_from_checkpoint("tcn_model")
return model
[ ]:
model = build_fit_tcn_model(
in_len=7 * DAY_DURATION,
out_len=6 * DAY_DURATION,
kernel_size=5,
num_filters=5,
weight_norm=False,
dilation_base=2,
dropout=0.2,
lr=1e-3,
include_dayofweek=True,
)
[10]:
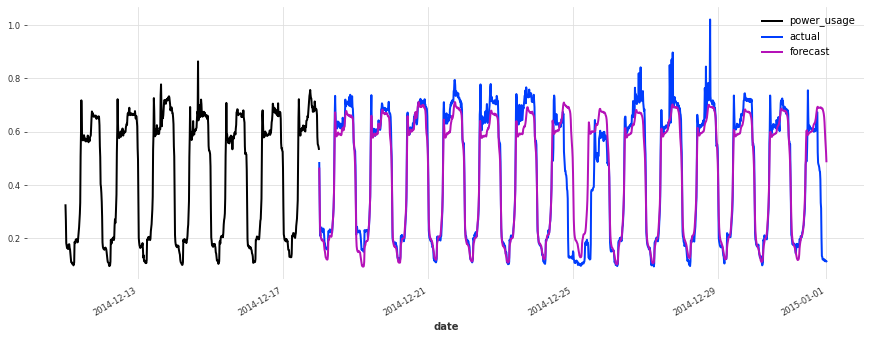
preds = model.predict(series=train, n=val_len)
eval_model(preds, "First TCN model")
GPU available: True, used: True
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0]
First TCN model sMAPE: 16.94 +- 20.03

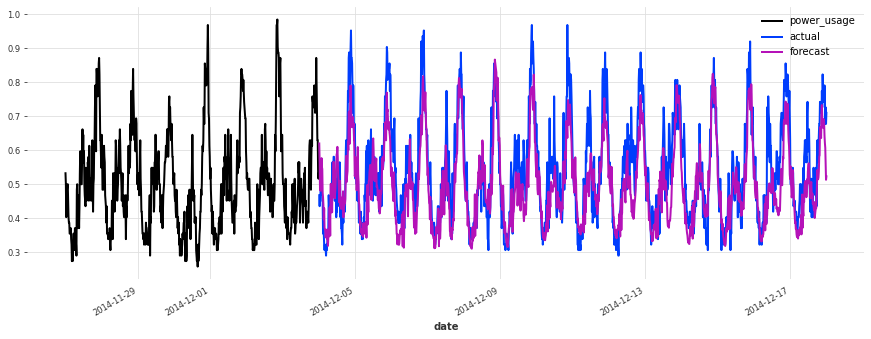
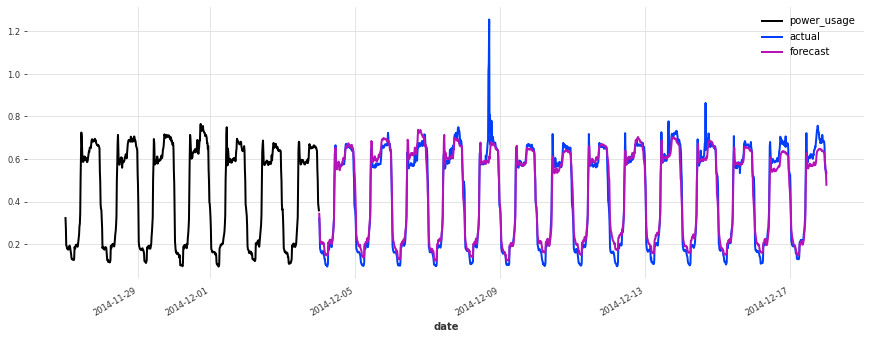
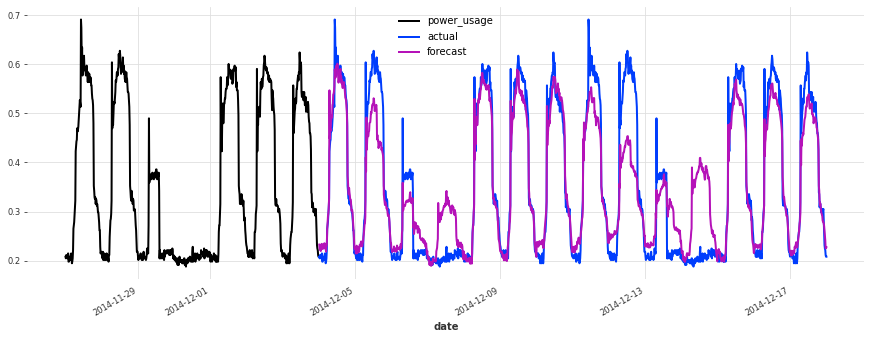
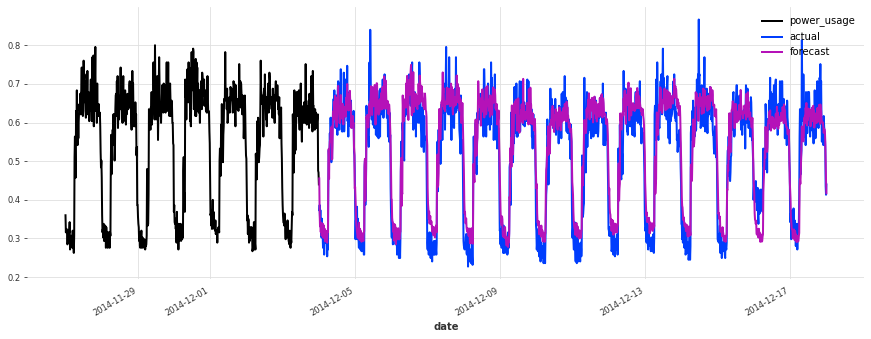
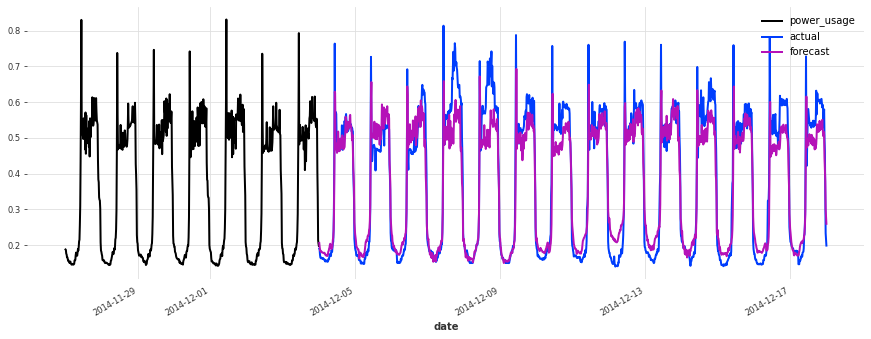
上面,我们构建了第一个 TCN 模型,没有进行任何超参数搜索,sMAPE 约为 17%。尽管此模型看起来是一个好的开始(在某些序列上表现相当不错),但它不如简单的线性回归。
我们肯定可以做得更好,因为我们已经固定了许多参数,但它们可能对性能产生巨大影响,例如:
网络的架构(滤波器数量、扩张大小、核大小等...)
学习率
是否使用权重归一化和/或 Dropout 率
回溯和前瞻窗口的长度
是否添加日历协变量,例如星期几
…
一种选择:使用 gridsearch()¶
尝试优化这些超参数的一种方法是尝试所有组合(假设我们已经将参数离散化)。Darts 提供了一个 gridsearch() 方法来执行此操作。优点是它非常易于使用。然而,它也有严重的缺点:
它所需时间随超参数数量呈指数增长:因此,对任何非平凡数量的超参数进行网格搜索很快就变得无法处理。
网格搜索是天真的:它不尝试关注超参数空间中比其他区域更有希望的区域。它仅限于预定义网格中的点。
最后,出于简单性考虑,Darts 的
gridsearch()方法(至少在撰写本文时)仅限于处理一个时间序列。
由于所有这些原因,对于任何严肃的超参数搜索,我们需要比网格搜索更好的技术。幸运的是,有一些很棒的工具可以帮助我们。
使用 Optuna¶
Optuna 是一个非常优秀的开源超参数优化库。它基于贝叶斯优化等思想,平衡了探索(超参数空间)与利用(即更多地探索那些看起来更有前景的空间区域)。它还可以使用剪枝功能,以便提前停止没有前途的实验。
让它工作非常简单:Optuna 将负责为我们建议(采样)超参数,而我们需要做的基本上就是计算一组超参数的目标值。在我们的案例中,这包括使用这些超参数构建模型、训练模型,并报告获得的验证准确率。我们还设置了一个 PyTorch Lightning 剪枝回调函数,以便提前停止没有前途的实验。所有这些都在下面的 objective() 函数中完成。
[16]:
def objective(trial):
callback = [PyTorchLightningPruningCallback(trial, monitor="val_loss")]
# set input_chunk_length, between 5 and 14 days
days_in = trial.suggest_int("days_in", 5, 14)
in_len = days_in * DAY_DURATION
# set out_len, between 1 and 13 days (it has to be strictly shorter than in_len).
days_out = trial.suggest_int("days_out", 1, days_in - 1)
out_len = days_out * DAY_DURATION
# Other hyperparameters
kernel_size = trial.suggest_int("kernel_size", 5, 25)
num_filters = trial.suggest_int("num_filters", 5, 25)
weight_norm = trial.suggest_categorical("weight_norm", [False, True])
dilation_base = trial.suggest_int("dilation_base", 2, 4)
dropout = trial.suggest_float("dropout", 0.0, 0.4)
lr = trial.suggest_float("lr", 5e-5, 1e-3, log=True)
include_dayofweek = trial.suggest_categorical("dayofweek", [False, True])
# build and train the TCN model with these hyper-parameters:
model = build_fit_tcn_model(
in_len=in_len,
out_len=out_len,
kernel_size=kernel_size,
num_filters=num_filters,
weight_norm=weight_norm,
dilation_base=dilation_base,
dropout=dropout,
lr=lr,
include_dayofweek=include_dayofweek,
callbacks=callback,
)
# Evaluate how good it is on the validation set
preds = model.predict(series=train, n=val_len)
smapes = smape(val, preds, n_jobs=-1, verbose=True)
smape_val = np.mean(smapes)
return smape_val if smape_val != np.nan else float("inf")
现在我们已经指定了目标,我们需要做的就是创建一个 Optuna 研究,并运行优化。我们可以要求 Optuna 运行指定的时间(如我们在此处所做),或者运行一定数量的试验。让我们运行优化几个小时
[ ]:
def print_callback(study, trial):
print(f"Current value: {trial.value}, Current params: {trial.params}")
print(f"Best value: {study.best_value}, Best params: {study.best_trial.params}")
study = optuna.create_study(direction="minimize")
study.optimize(objective, timeout=7200, callbacks=[print_callback])
# We could also have used a command as follows to limit the number of trials instead:
# study.optimize(objective, n_trials=100, callbacks=[print_callback])
# Finally, print the best value and best hyperparameters:
print(f"Best value: {study.best_value}, Best params: {study.best_trial.params}")
注意:如果我们想进一步优化,我们仍然可以多次调用 study.optimize() 从上次中断的地方继续。
使用 Optuna 您还可以做更多事情。有关更多信息,请参阅其文档。例如,可以通过可视化目标值历史(跨试验)、目标值作为某些超参数的函数,或某些超参数的总体重要性来获取有关优化过程的有用见解。
[16]:
plot_optimization_history(study)
[18]:
plot_contour(study, params=["lr", "num_filters"])
[19]:
plot_param_importances(study)
选择最佳模型¶
在 GPU 上运行超参数优化几个小时后,我们得到了:
Best value: 14.720555851487694, Best params: {'days_in': 14, 'days_out': 6, 'kernel_size': 19, 'num_filters': 19, 'weight_norm': True, 'dilation_base': 4, 'dropout': 0.07718156729165897, 'lr': 0.0008841998396117885, 'dayofweek': False}
现在我们可以使用这些超参数再次训练“最佳”模型。这次,我们将直接尝试拟合一个概率模型(使用高斯似然)。请注意,这实际上改变了损失函数,因此我们希望我们的超参数在这方面不太敏感。
[ ]:
best_model = build_fit_tcn_model(
in_len=14 * DAY_DURATION,
out_len=6 * DAY_DURATION,
kernel_size=19,
num_filters=19,
weight_norm=True,
dilation_base=4,
dropout=0.0772,
lr=0.0008842,
likelihood=GaussianLikelihood(),
include_dayofweek=False,
)
现在让我们看看随机预测的准确性,使用 100 个样本:
[51]:
best_preds = best_model.predict(
series=train, n=val_len, num_samples=100, mc_dropout=True
)
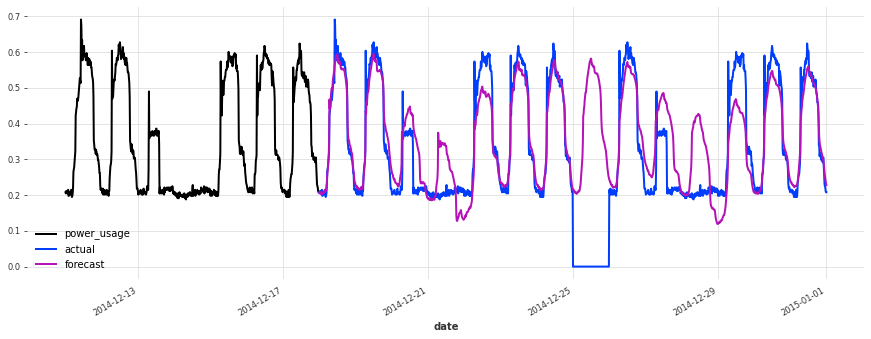
eval_model(best_preds, "best model, probabilistic")
LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0]
best model, probabilistic sMAPE: 15.21 +- 19.76
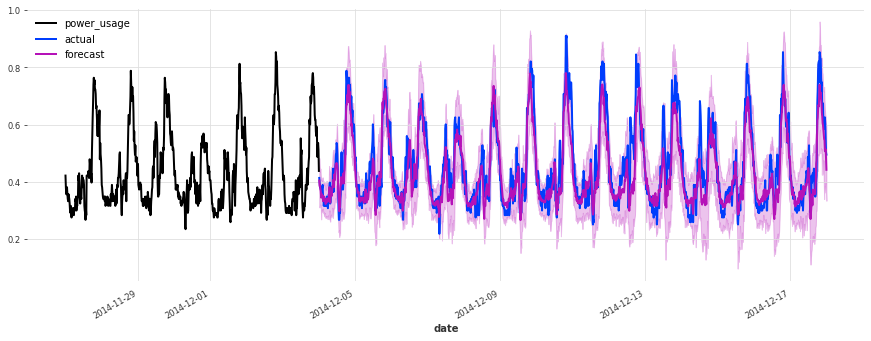
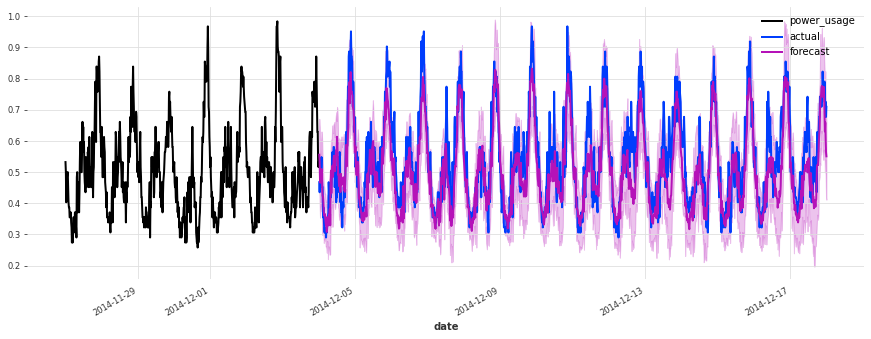
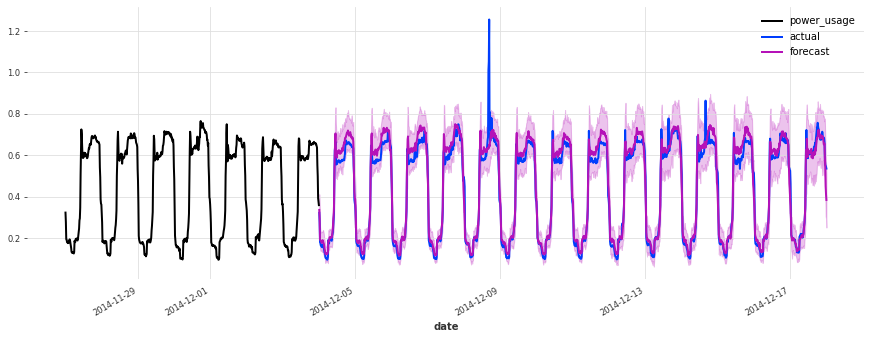
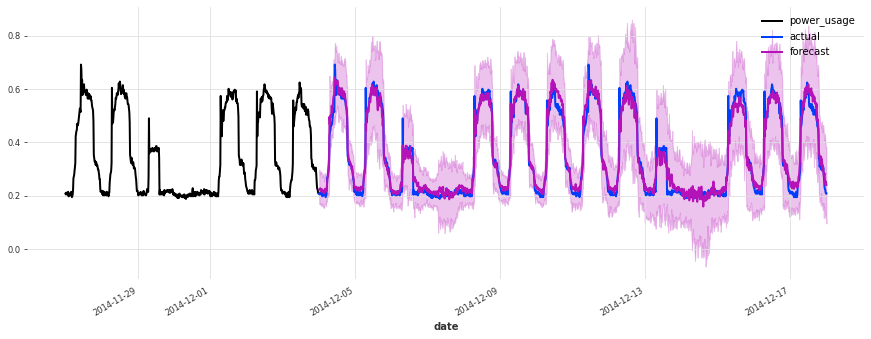
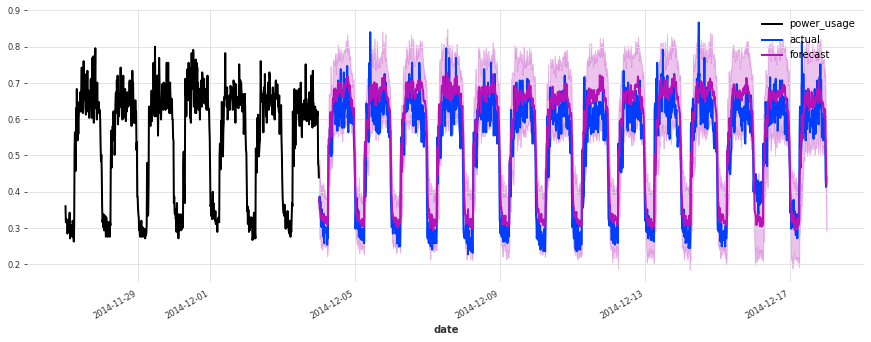
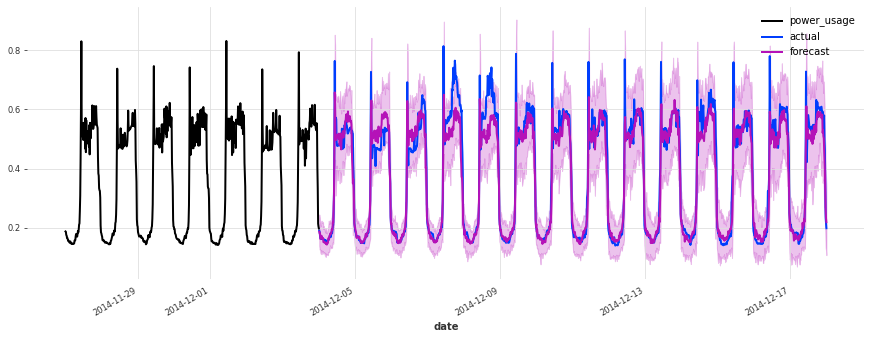
准确性看起来确实很好,而且这个模型没有遇到我们最初的线性回归和早期 TCN 模型遇到的一些相同问题(例如,看看它在序列 150 上曾经出现的失败模式)。
现在让我们也看看它在测试集上的表现如何:
[50]:
train_val_set = scaler.transform([s[:-val_len] for s in all_series_fp32])
best_preds_test = best_model.predict(
series=train_val_set, n=val_len, num_samples=100, mc_dropout=True
)
eval_model(
best_preds_test,
"best model, probabilistic, on test set",
train_set=train_val_set,
val_set=test,
)
LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0]
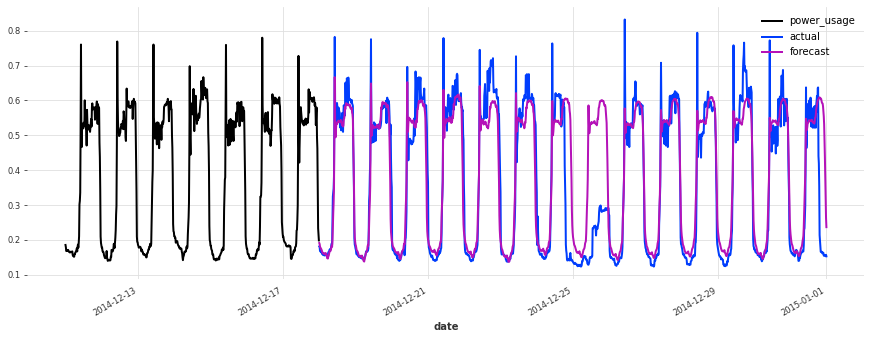
best model, probabilistic, on test set sMAPE: 19.21 +- 21.43
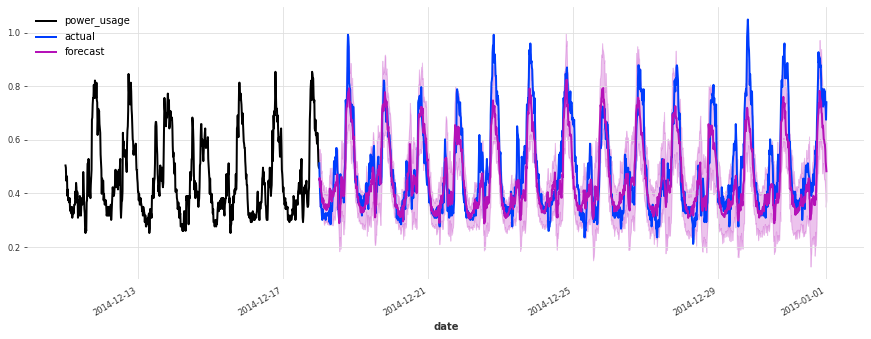
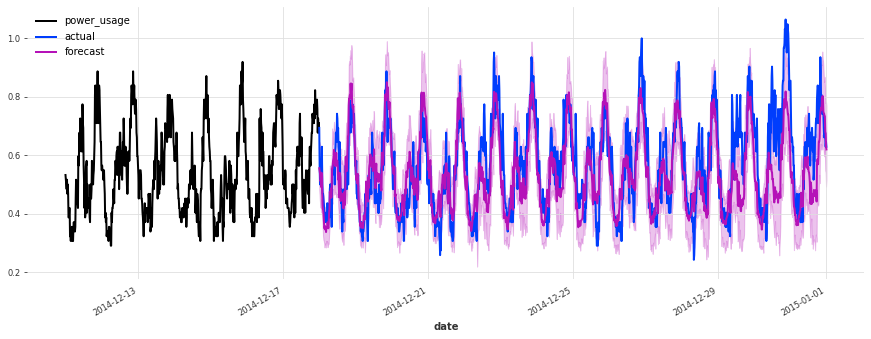
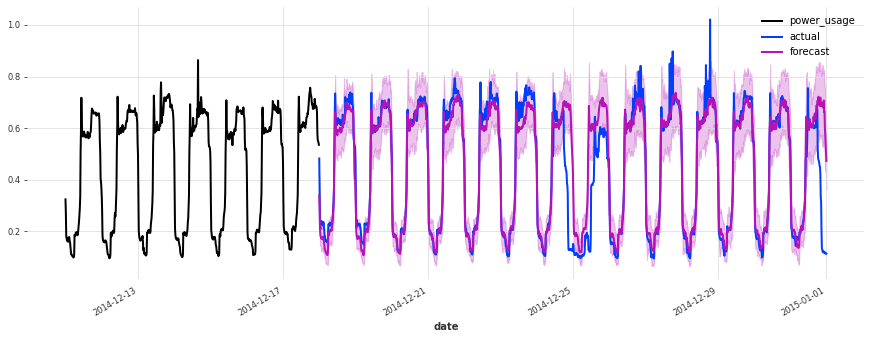
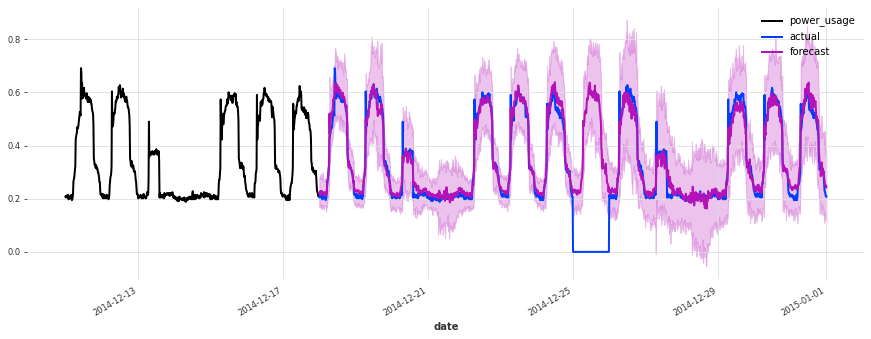
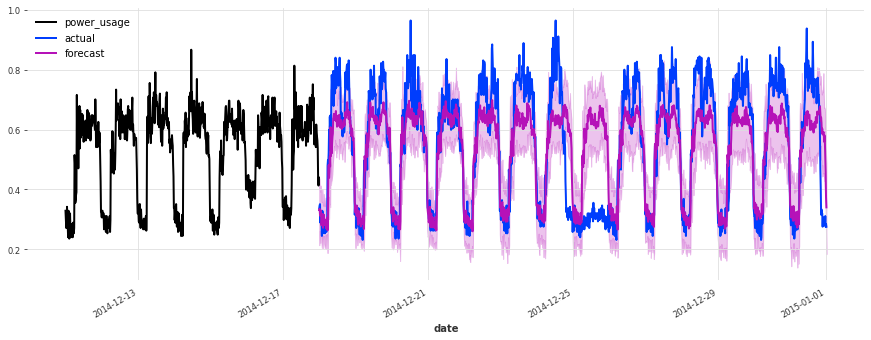
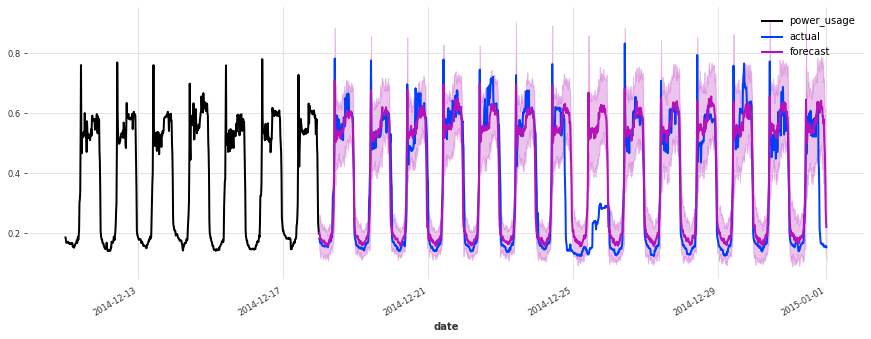
在测试集上的表现不如验证集,但仔细检查发现这似乎是由于圣诞节期间,一些客户(不足为奇地)改变了他们的消费习惯。除了圣诞节期间,预测的质量似乎与验证集期间大致相当,这很好地表明我们可能没有将超参数优化过度拟合到验证集上。
为了进一步改进此模型,考虑使用捕获公共假期的指标变量(我们在此处尚未这样做)可能是一个好主意。
作为最后一个实验,让我们看看我们的线性回归模型在测试集上的表现如何:
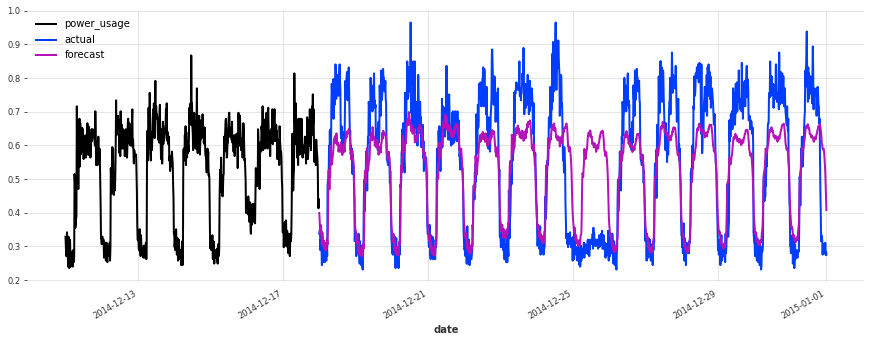
[43]:
lr_model = LinearRegressionModel(lags=7 * DAY_DURATION)
lr_preds_test = lr_model.predict(series=train_val_set, n=val_len)
eval_model(
lr_preds_test,
"linear regression, on test set",
train_set=train_val_set,
val_set=test,
)
linear regression, on test set sMAPE: 20.07 +- 22.67
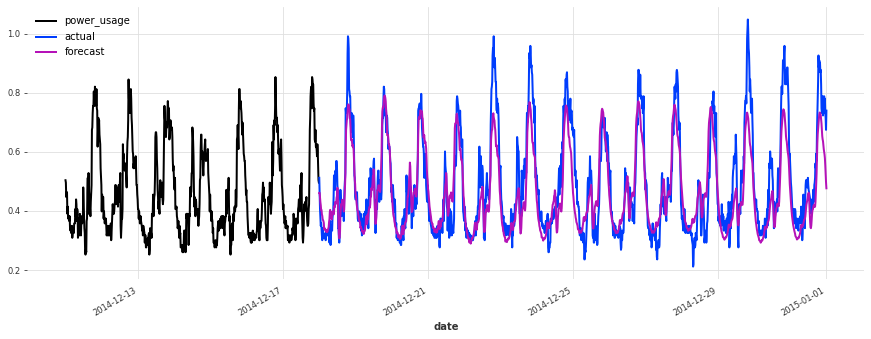
结论¶
在本 notebook 中,我们看到 Optuna 可以无缝地用于优化 Darts 模型的超参数。实际上,对于超参数优化而言,Darts 并没有什么特别之处:Optuna 和其他库可以像用于其他框架一样使用。唯一需要注意的是 PyTorch Lightning 集成,它通过 Darts 提供。
附带结论:我们应该选择线性回归还是 TCN 来预测电力消耗?¶
这两种方法都有优缺点。
线性回归的优点
简单
不需要缩放
速度快
不需要 GPU
通常开箱即用表现良好,无需调优
线性回归的缺点
可能需要大量内存(在此处用作全局模型时),尽管有解决方法(例如,基于 SGD 的)。
在我们的设置中,训练
LinearRegression模型的随机版本是不切实际的,因为这将导致过高的计算复杂度。
TCN 的优点
潜力更大,更易于调优
由于 SGD,通常内存需求较低
提供非常丰富的支持,以不同方式捕获随机性,而无需显著增加计算量
模型训练完成后,对多个时间序列进行批量推断非常快 - 特别是使用 GPU 时
TCN 的缺点
超参数更多,调优时间更长,过拟合风险更高。这也意味着模型更难工业化和维护
通常需要 GPU
[ ]: