概率性 RNN

在本 notebook 中，我们将展示一个概率性 RNN 如何与 darts 一起使用的示例。这种类型的 RNN 受 DeepAR 启发，并且与其几乎相同：https://arxiv.org/abs/1704.04110

# fix python path if working locally
from utils import fix_pythonpath_if_working_locally

fix_pythonpath_if_working_locally()

%load_ext autoreload
%autoreload 2
%matplotlib inline

import warnings

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

import darts.utils.timeseries_generation as tg
from darts import TimeSeries
from darts.dataprocessing.transformers import Scaler
from darts.datasets import EnergyDataset
from darts.models import RNNModel
from darts.timeseries import concatenate
from darts.utils.callbacks import TFMProgressBar
from darts.utils.likelihood_models.torch import GaussianLikelihood
from darts.utils.missing_values import fill_missing_values
from darts.utils.timeseries_generation import datetime_attribute_timeseries

warnings.filterwarnings("ignore")
import logging

logging.disable(logging.CRITICAL)


def generate_torch_kwargs():
    # run torch models on CPU, and disable progress bars for all model stages except training.
    return {
        "pl_trainer_kwargs": {
            "accelerator": "cpu",
            "callbacks": [TFMProgressBar(enable_train_bar_only=True)],
        }
    }

可变噪声序列

作为一个玩具示例，我们创建一个目标时间序列，它是由正弦波和高斯噪声序列相加而成的。为了增加趣味性，高斯噪声的强度也由一个正弦波（频率不同）进行调制。这意味着噪声的影响会以振荡的方式变强和变弱。其目的是测试概率性 RNN 是否能够在其预测中模拟这种振荡的不确定性。

length = 400
trend = tg.linear_timeseries(length=length, end_value=4)
season1 = tg.sine_timeseries(length=length, value_frequency=0.05, value_amplitude=1.0)
noise = tg.gaussian_timeseries(length=length, std=0.6)
noise_modulator = (
    tg.sine_timeseries(length=length, value_frequency=0.02)
    + tg.constant_timeseries(length=length, value=1)
) / 2
noise = noise * noise_modulator

target_series = sum([noise, season1])
covariates = noise_modulator
target_train, target_val = target_series.split_after(0.65)

target_train.plot()
target_val.plot()

<Axes: xlabel='time'>

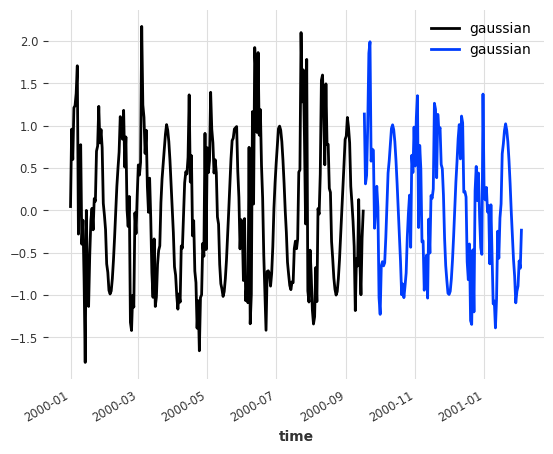
接下来，我们将训练一个概率性 RNN 以自回归方式预测目标序列，同时也将噪声分量的调制作为未来已知的协变量加以考虑。因此，RNN 知道目标序列的噪声分量何时会很严重，但它不知道噪声分量本身。让我们看看 RNN 是否能利用这些信息。

my_model = RNNModel(
    model="LSTM",
    hidden_dim=20,
    dropout=0,
    batch_size=16,
    n_epochs=50,
    optimizer_kwargs={"lr": 1e-3},
    random_state=0,
    training_length=50,
    input_chunk_length=20,
    likelihood=GaussianLikelihood(),
    **generate_torch_kwargs(),
)

my_model.fit(target_train, future_covariates=covariates)

RNNModel(model=LSTM, hidden_dim=20, n_rnn_layers=1, dropout=0, training_length=50, batch_size=16, n_epochs=50, optimizer_kwargs={'lr': 0.001}, random_state=0, input_chunk_length=20, likelihood=GaussianLikelihood(prior_mu=None, prior_sigma=None, prior_strength=1.0, beta_nll=0.0), pl_trainer_kwargs={'accelerator': 'cpu', 'callbacks': [<darts.utils.callbacks.TFMProgressBar object at 0x2b3386350>]})

pred = my_model.predict(80, num_samples=50)
target_val.slice_intersect(pred).plot(label="target")
pred.plot(label="prediction")

<Axes: xlabel='time'>

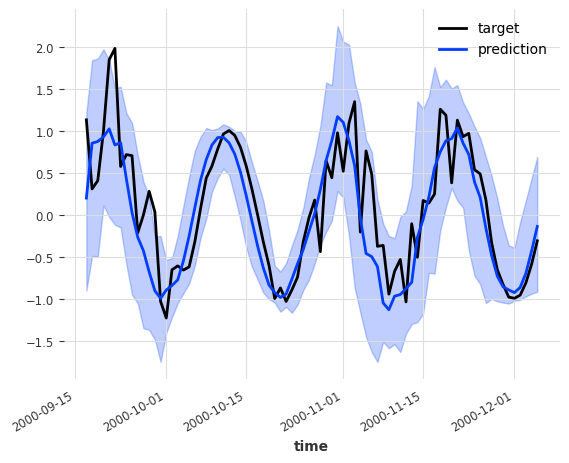
我们可以看到，除了正确预测目标的简单振荡行为外，RNN 在噪声分量较高时，其预测中也正确地表达了更多不确定性。

日常能源生产

df3 = EnergyDataset().load().to_dataframe()
df3_day_avg = (
    df3.groupby(df3.index.astype(str).str.split(" ").str[0]).mean().reset_index()
)
series_en = fill_missing_values(
    TimeSeries.from_dataframe(
        df3_day_avg, "time", ["generation hydro run-of-river and poundage"]
    ),
    "auto",
)

# convert to float32
series_en = series_en.astype(np.float32)

# create train and test splits
train_en, val_en = series_en.split_after(pd.Timestamp("20170901"))

# scale
scaler_en = Scaler()
train_en_transformed = scaler_en.fit_transform(train_en)
val_en_transformed = scaler_en.transform(val_en)
series_en_transformed = scaler_en.transform(series_en)

# add the day as a covariate (no scaling required as the day is one-hot-encoded)
day_series = datetime_attribute_timeseries(
    series_en, attribute="day", one_hot=True, dtype=np.float32
)

plt.figure(figsize=(10, 3))
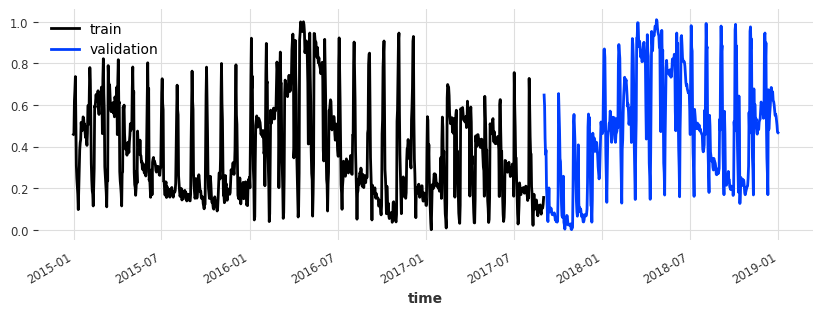
train_en_transformed.plot(label="train")
val_en_transformed.plot(label="validation")

<Axes: xlabel='time'>

model_name = "LSTM_test"
model_en = RNNModel(
    model="LSTM",
    hidden_dim=20,
    n_rnn_layers=2,
    dropout=0.2,
    batch_size=16,
    n_epochs=10,
    optimizer_kwargs={"lr": 1e-3},
    random_state=0,
    training_length=300,
    input_chunk_length=300,
    likelihood=GaussianLikelihood(),
    model_name=model_name,
    save_checkpoints=True,  # store the latest and best performing epochs
    force_reset=True,
    **generate_torch_kwargs(),
)

model_en.fit(
    series=train_en_transformed,
    future_covariates=day_series,
    val_series=val_en_transformed,
    val_future_covariates=day_series,
)

RNNModel(model=LSTM, hidden_dim=20, n_rnn_layers=2, dropout=0.2, training_length=300, batch_size=16, n_epochs=10, optimizer_kwargs={'lr': 0.001}, random_state=0, input_chunk_length=300, likelihood=GaussianLikelihood(prior_mu=None, prior_sigma=None, prior_strength=1.0, beta_nll=0.0), model_name=LSTM_test, save_checkpoints=True, force_reset=True, pl_trainer_kwargs={'accelerator': 'cpu', 'callbacks': [<darts.utils.callbacks.TFMProgressBar object at 0x2c1c97a00>]})

让我们加载处于最佳性能状态的模型

model_en = RNNModel.load_from_checkpoint(model_name=model_name, best=True)

现在我们进行历史预测： - 我们从验证序列的开头开始预测 (start=val_en_transformed.start_time()) - 每个预测的长度为 forecast_horizon=30。 - 下一个预测将从向前 stride=30 个点开始 - 我们保留每次预测的所有预测值 (last_points_only=False) - 继续直到输入数据用完

最后，我们将历史预测进行连接，得到一个单一的连续（时间轴上）时间序列

backtest_en = model_en.historical_forecasts(
    series=series_en_transformed,
    future_covariates=day_series,
    start=val_en_transformed.start_time(),
    num_samples=500,
    forecast_horizon=30,
    stride=30,
    retrain=False,
    verbose=True,
    last_points_only=False,
)
backtest_en = concatenate(backtest_en, axis=0)

plt.figure(figsize=(10, 6))
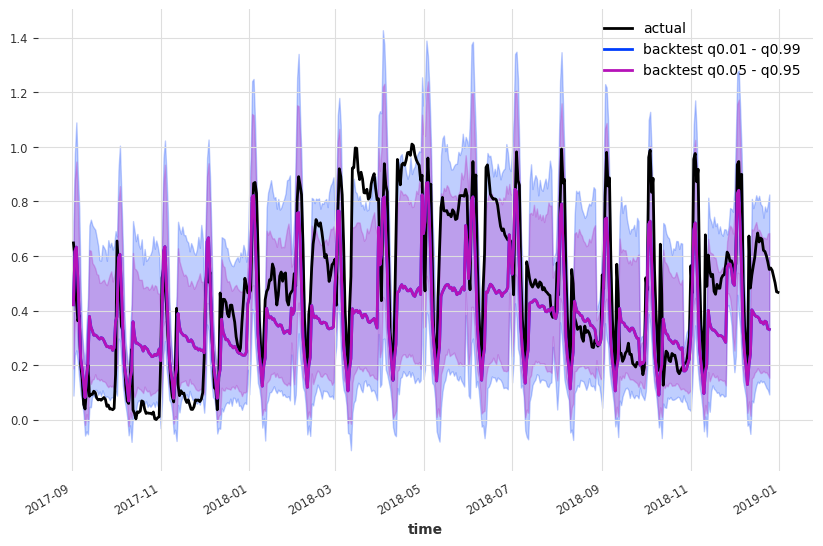
val_en_transformed.plot(label="actual")
backtest_en.plot(label="backtest q0.01 - q0.99", low_quantile=0.01, high_quantile=0.99)
backtest_en.plot(label="backtest q0.05 - q0.95", low_quantile=0.05, high_quantile=0.95)
plt.legend()

<matplotlib.legend.Legend at 0x2c0581de0>

上一页

N-BEATS

下一页

DeepTCN 模型